ExpandAddress
Introduction: Returns an array of expanded forms of the input address string. This is backed by the libpostal library’s address expanding functionality. Format:ExpandAddress (address: String)
SQL Example
ParseAddress
Introduction: Returns an array of the components (e.g. street, postal code) of the input address string. This is backed by the libpostal library’s address parsing functionality. Format:ParseAddress (address: String)
SQL Example
GeometryType
Introduction: Returns the type of the geometry as a string. Eg: ‘LINESTRING’, ‘POLYGON’, ‘MULTIPOINT’, etc. This function also indicates if the geometry is measured, by returning a string of the form ‘POINTM’. Format:GeometryType (A: Geometry)
SQL Example
ST_3DDistance
Introduction: Return the 3-dimensional minimum cartesian distance between A and B Format:ST_3DDistance (A: Geometry, B: Geometry)
SQL Example
ST_AddMeasure
Introduction: Computes a new geometry with measure (M) values linearly interpolated between start and end points. For geometries lacking M dimensions, M values are added. Existing M values are overwritten by the new values. Applies only to LineString and MultiLineString inputs. Format:ST_AddMeasure(geom: Geometry, measureStart: Double, measureEnd: Double)
SQL Example:
ST_AddPoint
Introduction: RETURN Linestring with additional point at the given index, if position is not available the point will be added at the end of line. Format:ST_AddPoint(geom: Geometry, point: Geometry, position: Integer)
ST_AddPoint(geom: Geometry, point: Geometry)
SQL Example
ST_Affine
Introduction: Apply an affine transformation to the given geometry. ST_Affine has 2 overloaded signatures:ST_Affine(geometry, a, b, c, d, e, f, g, h, i, xOff, yOff, zOff)
ST_Affine(geometry, a, b, d, e, xOff, yOff)
Based on the invoked function, the following transformation is applied:
x = a * x + b * y + c * z + xOff OR x = a * x + b * y + xOff
y = d * x + e * y + f * z + yOff OR y = d * x + e * y + yOff
z = g * x + f * y + i * z + zOff OR z = g * x + f * y + zOff
If the given geometry is empty, the result is also empty.
Format:
ST_Affine(geometry, a, b, c, d, e, f, g, h, i, xOff, yOff, zOff)
ST_Affine(geometry, a, b, d, e, xOff, yOff)
LINESTRING EMPTY
Output: LINESTRING EMPTY
Input: POLYGON ((1 0 1, 1 1 1, 2 2 2, 1 0 1))
Output: POLYGON Z((9 11 11, 11 12 13, 18 16 23, 9 11 11))
Input: POLYGON ((1 0, 1 1, 2 1, 2 0, 1 0), (1 0.5, 1 0.75, 1.5 0.75, 1.5 0.5, 1 0.5))
Output: POLYGON((5 9, 7 10, 8 11, 6 10, 5 9), (6 9.5, 6.5 9.75, 7 10.25, 6.5 10, 6 9.5))
POLYGON EMPTY
Output: POLYGON EMPTY
Input: GEOMETRYCOLLECTION (MULTIPOLYGON (((1 0, 1 1, 2 1, 2 0, 1 0), (1 0.5, 1 0.75, 1.5 0.75, 1.5 0.5, 1 0.5)), ((5 0, 5 5, 7 5, 7 0, 5 0))), POINT (10 10))
Output: GEOMETRYCOLLECTION (MULTIPOLYGON (((2 3, 4 5, 5 6, 3 4, 2 3), (3 4, 3.5 4.5, 4 5, 3.5 4.5, 3 4)), ((6 7, 16 17, 18 19, 8 9, 6 7))), POINT (31 32))
Input: POLYGON ((1 0 1, 1 1 1, 2 2 2, 1 0 1))
Output: POLYGON Z((2 3 1, 4 5 1, 7 8 2, 2 3 1))
ST_Angle
Introduction: Computes and returns the angle between two vectors represented by the provided points or linestrings. There are three variants possible for ST_Angle:ST_Angle(point1: Geometry, point2: Geometry, point3: Geometry, point4: Geometry)
Computes the angle formed by vectors represented by point1 - point2 and point3 - point4
ST_Angle(point1: Geometry, point2: Geometry, point3: Geometry)
Computes the angle formed by vectors represented by point2 - point1 and point2 - point3
ST_Angle(line1: Geometry, line2: Geometry)
Computes the angle formed by vectors S1 - E1 and S2 - E2, where S and E denote start and end points respectively
If any other geometry type is provided, ST_Angle throws an IllegalArgumentException.
Additionally, if any of the provided geometry is empty, ST_Angle throws an IllegalArgumentException.
If a 3D geometry is provided, ST_Angle computes the angle ignoring the z ordinate, equivalent to calling ST_Angle for corresponding 2D geometries.
ST_Angle(p1, p2, p3, p4) | ST_Angle(p1, p2, p3) | ST_Angle(line1, line2)
SQL Example
ST_Area
Introduction: Return the area of A Format:ST_Area (A: Geometry)
SQL Example
ST_AreaSpheroid
Introduction: Return the geodesic area of A using WGS84 spheroid. Unit is square meter. Works better for large geometries (country level) compared toST_Area + ST_Transform. It is equivalent to PostGIS ST_Area(geography, use_spheroid=true) function and produces nearly identical results.
Geometry must be in EPSG:4326 (WGS84) projection and must be in ==lon/lat== order. You can use ==ST_FlipCoordinates== to swap lat and lon.
By default, this function uses lon/lat order.
ST_AreaSpheroid (A: Geometry)
SQL Example
ST_AsBinary
Introduction: Return the Well-Known Binary representation of a geometry Format:ST_AsBinary (A: Geometry)
SQL Example
ST_AsEWKB
Introduction: Return the Extended Well-Known Binary representation of a geometry. EWKB is an extended version of WKB which includes the SRID of the geometry. The format originated in PostGIS but is supported by many GIS tools. If the geometry is lacking SRID a WKB format is produced. See ST_SetSRID It will ignore the M coordinate if present. Format:ST_AsEWKB (A: Geometry)
SQL Example
ST_AsEWKT
Introduction: Return the Extended Well-Known Text representation of a geometry. EWKT is an extended version of WKT which includes the SRID of the geometry. The format originated in PostGIS but is supported by many GIS tools. If the geometry is lacking SRID a WKT format is produced. See ST_SetSRID It will support M coordinate if present. Format:ST_AsEWKT (A: Geometry)
SQL Example
ST_AsGeoJSON
Introduction: Return the GeoJSON string representation of a geometry The type parameter takes the following options -- “Simple” (default): Returns a simple GeoJSON geometry.
- “Feature”: Wraps the geometry in a GeoJSON Feature.
- “FeatureCollection”: Wraps the Feature in a GeoJSON FeatureCollection.
ST_AsGeoJSON (A: Geometry)
ST_AsGeoJSON (A: Geometry, type: String)
SQL Example (Simple GeoJSON):
ST_AsGML
Introduction: Return the GML string representation of a geometry Format:ST_AsGML (A: Geometry)
SQL Example
ST_AsHEXEWKB
Introduction: This function returns the input geometry encoded to a text representation in HEXEWKB format. The HEXEWKB encoding can use either little-endian (NDR) or big-endian (XDR) byte ordering. If no encoding is explicitly specified, the function defaults to using the little-endian (NDR) format. Format:ST_AsHEXEWKB(geom: Geometry, endian: String = NDR)
SQL Example
ST_AsKML
Introduction: Return the KML string representation of a geometry Format:ST_AsKML (A: Geometry)
SQL Example
ST_AsText
Introduction: Return the Well-Known Text string representation of a geometry. It will support M coordinate if present. Format:ST_AsText (A: Geometry)
SQL Example
ST_Azimuth
Introduction: Returns Azimuth for two given points in radians null otherwise. Format:ST_Azimuth(pointA: Point, pointB: Point)
SQL Example
ST_BestSRID
Introduction: Returns the estimated most appropriate Spatial Reference Identifier (SRID) for a given geometry, based on its spatial extent and location. It evaluates the geometry’s bounding envelope and selects an SRID that optimally represents the geometry on the Earth’s surface. The function prioritizes Universal Transverse Mercator (UTM), Lambert Azimuthal Equal Area (LAEA), or falls back to the Mercator projection. The function takes a WGS84 geometry and must be in ==lon/lat== order.- For geometries in the Arctic or Antarctic regions, the Lambert Azimuthal Equal Area projection is used.
- For geometries that fit within a single UTM zone and do not cross the International Date Line (IDL), a corresponding UTM SRID is chosen.
- In cases where none of the above conditions are met, the function defaults to the Mercator projection.
- For Geometries that cross the IDL,
ST_BestSRIDdefaults the SRID to Mercator. Currently,ST_BestSRIDdoes not handle geometries crossing the IDL.
ST_BestSRID(geom: Geometry)
SQL Example:
ST_BinaryDistanceBandColumn
Introduction: Introduction: Returns aweights column containing every record in a dataframe within a specified threshold distance.
The weights column is an array of structs containing the attributes from each neighbor and that neighbor’s weight. Since this is a binary distance band function, weights of neighbors within the threshold will always be
1.0.
Format: ST_BinaryDistanceBandColumn(geometry:Geometry, threshold: Double, includeZeroDistanceNeighbors: boolean, includeSelf: boolean, useSpheroid: boolean, attributes: Struct)
SQL Example
ST_Boundary
Introduction: Returns the closure of the combinatorial boundary of this Geometry. Format:ST_Boundary(geom: Geometry)
SQL Example
ST_BoundingDiagonal
Introduction: Returns a linestring spanning minimum and maximum values of each dimension of the given geometry’s coordinates as its start and end point respectively. If an empty geometry is provided, the returned LineString is also empty. If a single vertex (POINT) is provided, the returned LineString has both the start and end points same as the points coordinates Format:ST_BoundingDiagonal(geom: Geometry)
SQL Example
POLYGON ((1 1 1, 3 3 3, 0 1 4, 4 4 0, 1 1 1))
Output: LINESTRING Z(0 1 1, 4 4 4)
Input: POINT (10 10)
Output: LINESTRING (10 10, 10 10)
Input: GEOMETRYCOLLECTION(POLYGON ((5 5 5, -1 2 3, -1 -1 0, 5 5 5)), POINT (10 3 3))
Output: LINESTRING Z(-1 -1 0, 10 5 5)
ST_Buffer
Introduction: Returns a geometry/geography that represents all points whose distance from this Geometry/geography is less than or equal to distance. The function supports both Planar/Euclidean and Spheroidal/Geodesic buffering. Spheroidal buffer also supports geometries crossing the International Date Line (IDL). Mode of buffer calculation: The optional third parameter,useSpheroid, controls the mode of buffer calculation.
- Planar Buffering (default): When
useSpheroidis false,ST_Bufferperforms standard planar buffering based on the provided parameters. - Spheroidal Buffering:
- When
useSpheroidis set to true, the function returns the spheroidal buffer polygon for more accurate representation over the Earth. In this mode, the unit of the buffer distance is interpreted as meters. - ST_Buffer first determines the most appropriate Spatial Reference Identifier (SRID) for a given geometry, based on its spatial extent and location, using
ST_BestSRID. - The geometry is then transformed from its original SRID to the selected SRID. If the input geometry does not have a set SRID,
ST_Bufferdefaults to using WGS 84 (SRID 4326) as its original SRID. - The standard planar buffer operation is then applied in this coordinate system.
- Finally, the buffered geometry is transformed back to its original SRID, or to WGS 84 if the original SRID was not set.
- When
As of now, spheroidal buffering only supports lon/lat coordinate systems and will throw an
IllegalArgumentException for input geometries in meter based coordinate systems.Spheroidal buffering may not produce accurate output buffer for input geometries larger than a UTM zone.
quad_segs=#: Number of line segments utilized to approximate a quarter circle (default is 8).endcap=round|flat|square: End cap style (default isround).buttis an accepted synonym forflat.join=round|mitre|bevel: Join style (default isround).miteris an accepted synonym formitre.mitre_limit=#.#: mitre ratio limit and it only affects mitred join style.miter_limitis an accepted synonym formitre_limit.side=both|left|right: The optionleftorrightenables a single-sided buffer operation on the geometry, with the buffered side aligned according to the direction of the line. This functionality is specific to LINESTRING geometry and has no impact on POINT or POLYGON geometries. By default, square end caps are applied.
ST_Buffer throws an IllegalArgumentException if the correct format, parameters, or options are not provided.
8 Segments
2 Segments
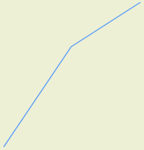
Original Linestring
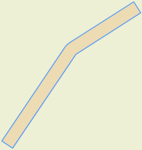
Left side buffed Linestring
ST_BuildArea
Introduction: Returns the areal geometry formed by the constituent linework of the input geometry. Format:ST_BuildArea (A: Geometry)
SQL Example
ST_Centroid
Introduction: Return the centroid point of A Format:ST_Centroid (A: Geometry)
SQL Example
ST_ClosestPoint
Introduction: Returns the 2-dimensional point on geom1 that is closest to geom2. This is the first point of the shortest line between the geometries. If using 3D geometries, the Z coordinates will be ignored. If you have a 3D Geometry, you may prefer to use ST_3DClosestPoint. It will throw an exception indicates illegal argument if one of the params is an empty geometry. Format:ST_ClosestPoint(g1: Geometry, g2: Geometry)
SQL Example
g1: POINT (160 40), g2: LINESTRING (10 30, 50 50, 30 110, 70 90, 180 140, 130 190)
Output: POINT(160 40)
Input: g1: LINESTRING (10 30, 50 50, 30 110, 70 90, 180 140, 130 190), g2: POINT (160 40)
Output: POINT(125.75342465753425 115.34246575342466)
Input: g1: 'POLYGON ((190 150, 20 10, 160 70, 190 150))', g2: ST_Buffer('POINT(80 160)', 30)
Output: POINT(131.59149149528952 101.89887534906197)
ST_Collect
Introduction: Returns MultiGeometry object based on geometry column/s or array with geometries Format:ST_Collect(*geom: Geometry)
ST_Collect(geom: ARRAY[Geometry])
SQL Example
ST_CollectionExtract
Introduction: Returns a homogeneous multi-geometry from a given geometry collection. The type numbers are:- POINT
- LINESTRING
- POLYGON
ST_CollectionExtract (A: Geometry)
ST_CollectionExtract (A: Geometry, type: Integer)
SQL Example
ST_ConcaveHull
Introduction: Return the Concave Hull of polygon A, with alpha set to pctConvex[0, 1] in the Delaunay Triangulation method, the concave hull will not contain a hole unless allowHoles is set to true Format:ST_ConcaveHull (A: Geometry, pctConvex: Double)
ST_ConcaveHull (A: Geometry, pctConvex: Double, allowHoles: Boolean)
SQL Example
ST_ConvexHull
Introduction: Return the Convex Hull of polygon A Format:ST_ConvexHull (A: Geometry)
SQL Example
ST_CoordDim
Introduction: Returns the coordinate dimensions of the geometry. It is an alias ofST_NDims.
Format: ST_CoordDim(geom: Geometry)
SQL Example with x, y, z coordinate:
ST_CrossesDateLine
Introduction: This function determines if a given geometry crosses the International Date Line. It operates by checking if the difference in longitude between any pair of consecutive points in the geometry exceeds 180 degrees. If such a difference is found, it is assumed that the geometry crosses the Date Line. It returns true if the geometry crosses the Date Line, and false otherwise.The function assumes that the provided geometry is in lon/lat coordinate reference system where longitude values range from -180 to 180 degrees.
For multi-geometries (e.g., MultiPolygon, MultiLineString), this function will return true if any one of the geometries within the multi-geometry crosses the International Date Line.
ST_CrossesDateLine(geometry: Geometry)
SQL Example:
ST_DBSCAN
Introduction: Performs a DBSCAN clustering across the entire dataframe. Returns a struct containing the cluster ID and a boolean indicating if the record is a core point in the cluster.epsilonis the maximum distance between two points for them to be considered as part of the same cluster.minPointsis the minimum number of neighbors a single record must have to form a cluster.useSpheroidis whether to use ST_DistanceSpheroid or ST_Distance as the distance metric.
ST_DBSCAN(geom: Geometry, epsilon: Double, minPoints: Integer, useSpheroid: Boolean)
Since: v1.7.1
SQL Example
ST_Degrees
Introduction: Convert an angle in radian to degrees. Format:ST_Degrees(angleInRadian)
SQL Example
ST_DelaunayTriangles
Introduction: This function computes the Delaunay triangulation for the set of vertices in the input geometry. An optionaltolerance parameter allows snapping nearby input vertices together prior to triangulation and can improve robustness in certain scenarios by handling near-coincident vertices. The default for tolerance is 0. The Delaunay triangulation geometry is bounded by the convex hull of the input vertex set.
The output geometry representation depends on the provided flag:
0- a GeometryCollection of triangular Polygons (default option)1- a MultiLinestring of the edges of the triangulation
ST_DelaunayTriangles(geometry: Geometry)
ST_DelaunayTriangles(geometry: Geometry, tolerance: Double)
ST_DelaunayTriangles(geometry: Geometry, tolerance: Double, flag: Integer)
SQL Example
ST_Difference
Introduction: Return the difference between geometry A and B (return part of geometry A that does not intersect geometry B) Format:ST_Difference (A: Geometry, B: Geometry)
SQL Example
ST_Dimension
Introduction: Return the topological dimension of this Geometry object, which must be less than or equal to the coordinate dimension. OGC SPEC s2.1.1.1 - returns 0 for POINT, 1 for LINESTRING, 2 for POLYGON, and the largest dimension of the components of a GEOMETRYCOLLECTION. If the dimension is unknown (e.g. for an empty GEOMETRYCOLLECTION) 0 is returned. Format:ST_Dimension (A: Geometry) | ST_Dimension (C: Geometrycollection)
SQL Example
ST_Distance
Introduction: Return the Euclidean distance between A and B Format:ST_Distance (A: Geometry, B: Geometry)
SQL Example
ST_DistanceSphere
Introduction: Returns the haversine / great-circle distance ofA using a given earth radius (default radius: 6371008.0). Unit is meters.
Compared to ST_Distance + ST_Transform, it works better for datasets that cover large regions such as continents or the entire planet.
It provides faster but less accurate result compared to ST_DistanceSpheroid.
Geometry must be in EPSG:4326 (WGS84) projection and must be in lon/lat order. You can use ST_FlipCoordinates to swap lat and lon.
For non-point data, we first take the centroids of both geometries and then compute the distance.
By default, this function uses lon/lat order.
ST_DistanceSphere (A: Geometry)
SQL Example
ST_DistanceSpheroid
Introduction: Return the geodesic distance of A using WGS84 spheroid. Unit is in meters. Compared toST_Distance + ST_Transform, it works better for datasets that cover large regions such as continents or the entire planet.
It provides slower but more accurate result compared to ST_DistanceSphere.
Geometry must be in EPSG:4326 (WGS84) projection and must be in ==lon/lat== order.
You can use ==ST_FlipCoordinates== to swap lat and lon. For non-point data, we first take the centroids of both geometries and then compute the distance.
By default, this function uses lon/lat order.
ST_DistanceSpheroid (A: Geometry)
SQL Example
ST_Dump
Introduction: It expands the geometries. If the geometry is simple (Point, Polygon Linestring etc.) it returns the geometry itself, if the geometry is collection or multi it returns record for each of collection components. Format:ST_Dump(geom: Geometry)
SQL Example
ST_DumpPoints
Introduction: Returns list of Points which geometry consists of. Format:ST_DumpPoints(geom: Geometry)
SQL Example
ST_EndPoint
Introduction: Returns last point of given linestring. Format:ST_EndPoint(geom: Geometry)
SQL Example
ST_Envelope
Introduction: Return the envelope boundary of A Format:ST_Envelope (A: Geometry)
SQL Example
ST_Expand
Introduction: Returns a geometry expanded from the bounding box of the input. The expansion can be specified in two ways:- By individual axis using
deltaX,deltaY, ordeltaZparameters. - Uniformly across all axes using the
uniformDeltaparameter.
Things to consider when using this function:
- The
uniformDeltaparameter expands Z dimensions for XYZ geometries; otherwise, it only affects XY dimensions. - For XYZ geometries, specifying only
deltaXanddeltaYwill preserve the original Z dimension. - If the input geometry has an M dimension then using this function will drop the said M dimension.
ST_Expand(geometry: Geometry, uniformDelta: Double)
ST_Expand(geometry: Geometry, deltaX: Double, deltaY: Double)
ST_Expand(geometry: Geometry, deltaX: Double, deltaY: Double, deltaZ: Double)
SQL Example:
ST_ExtentBasedSubDivide
Introduction: Return a list of geometries divided based of given extent limit. Format:- algMultiPoint:
decompose - algLineString:
cut_segments - algPolygon:
box_approx
maxVertices is 1000, and the omitted value for maxDepths is 50.
algorithms is a
string with 3 components: <algMultiPoint>/<algLineString>/<algPolygon>. The possible values for each components are:
algMultiPoint: Subdividing algorithm for MultiPoint
decompose: Simply decompose the MultiPoint to multiple Points. The number of subdivided geometries is determined by the number of points in the MultiPoint.packing: Use a simple heuristics to pack near by points together as smaller MultiPoints.
cut_segments: Cut the line segment to make sure that each subdivided LineString is no longer than a given threshold.preserve_segments: Don’t cut the segments, only split at the nodes of the LineString. The subdivided LineString could be a bit longer than the given threshold.
box_approx: Approximate the polygon with lots of boxes.overlay: Using the old JTS overlay implementation to clip polygons. Same asST_SubDivide.overlay_2: Using JTS overlay NG to clip polygons.triangulation: Using JTS triangulation algorithms to subdivide polygons.
ST_ExtentBasedSubDivideExplode
Introduction: It works the same as ST_ExtentBasedSubDivide but returns new rows with geometries instead of list. Format:ST_ExteriorRing
Introduction: Returns a line string representing the exterior ring of the POLYGON geometry. Return NULL if the geometry is not a polygon. Format:ST_ExteriorRing(geom: Geometry)
SQL Example
ST_FlipCoordinates
Introduction: Returns a version of the given geometry with X and Y axis flipped. Format:ST_FlipCoordinates(A: Geometry)
SQL Example
ST_Force_2D
Introduction: Forces the geometries into a “2-dimensional mode” so that all output representations will only have the X and Y coordinates. This function is an alias of ST_Force2D. Format:ST_Force_2D (A: Geometry)
SQL Example
ST_Force2D
Introduction: Forces the geometries into a “2-dimensional mode” so that all output representations will only have the X and Y coordinates. This function is an alias of ST_Force_2D. Format:ST_Force2D (A: Geometry)
SQL Example
ST_Force3D
Introduction: Forces the geometry into a 3-dimensional model so that all output representations will have X, Y and Z coordinates. An optionally given zValue is tacked onto the geometry if the geometry is 2-dimensional. Default value of zValue is 0.0 If the given geometry is 3-dimensional, no change is performed on it. If the given geometry is empty, no change is performed on it.Example output is after calling ST_AsText() on returned geometry, which adds Z for in the WKT for 3D geometries
ST_Force3D(geometry: Geometry, zValue: Double)
SQL Example
ST_Force3DM
Introduction: Forces the geometry into XYM mode. Retains any existing M coordinate, but removes the Z coordinate if present. Assigns a default M value of 0.0 ifmValue is not specified.
Example output is after calling ST_AsText() on returned geometry, which adds M for in the WKT.
ST_Force3DM(geometry: Geometry, mValue: Double = 0.0)
SQL Example
ST_Force3DZ
Introduction: Forces the geometry into a 3-dimensional model so that all output representations will have X, Y and Z coordinates. An optionally given zValue is tacked onto the geometry if the geometry is 2-dimensional. Default value of zValue is 0.0 If the given geometry is 3-dimensional, no change is performed on it. If the given geometry is empty, no change is performed on it. This function is an alias for ST_Force3D.Example output is after calling ST_AsText() on returned geometry, which adds Z for in the WKT for 3D geometries
ST_Force3DZ(geometry: Geometry, zValue: Double)
SQL Example
ST_Force4D
Introduction: Converts the input geometry to 4D XYZM representation. Retains original Z and M values if present. Assigning 0.0 defaults ifmValue and zValue aren’t specified. The output contains X, Y, Z, and M coordinates. For geometries already in 4D form, the function returns the original geometry unmodified.
Example output is after calling ST_AsText() on returned geometry, which adds Z for in the WKT for 3D geometries
ST_Force4D(geom: Geometry, zValue: Double, mValue: Double)
ST_Force4D(geom: Geometry
SQL Example
ST_ForceCollection
Introduction: This function converts the input geometry into a GeometryCollection, regardless of the original geometry type. If the input is a multipart geometry, such as a MultiPolygon or MultiLineString, it will be decomposed into a GeometryCollection containing each individual Polygon or LineString element from the original multipart geometry. Format:ST_ForceCollection(geom: Geometry)
SQL Example
ST_ForcePolygonCCW
Introduction: For (Multi)Polygon geometries, this function sets the exterior ring orientation to counter-clockwise and interior rings to clockwise orientation. Non-polygonal geometries are returned unchanged. Format:ST_ForcePolygonCCW(geom: Geometry)
SQL Example:
ST_ForcePolygonCW
Introduction: For (Multi)Polygon geometries, this function sets the exterior ring orientation to clockwise and interior rings to counter-clockwise orientation. Non-polygonal geometries are returned unchanged. Format:ST_ForcePolygonCW(geom: Geometry)
SQL Example:
ST_ForceRHR
Introduction: Sets the orientation of polygon vertex orderings to follow the Right-Hand-Rule convention. The exterior ring will have a clockwise winding order, while any interior rings are oriented counter-clockwise. This ensures the area bounded by the polygon falls on the right-hand side relative to the ring directions. The function is an alias for ST_ForcePolygonCW. Format:ST_ForceRHR(geom: Geometry)
SQL Example:
ST_FrechetDistance
Introduction: Computes and returns discrete Frechet Distance between the given two geometries, based on Computing Discrete Frechet Distance If any of the geometries is empty, returns 0.0 Format:ST_FrechetDistance(g1: Geometry, g2: Geometry)
SQL Example
ST_GeneratePoints
Introduction: Generates a specified quantity of pseudo-random points within the boundaries of the provided polygonal geometry. Whenseed is either zero or not defined then output will be random.
Format:
ST_GeneratePoints(geom: Geometry, numPoints: Integer, seed: Long = 0)
ST_GeneratePoints(geom: Geometry, numPoints: Integer)
SQL Example:
Due to the pseudo-random nature of point generation, the output of this function will vary between executions and may not match any provided examples.
ST_GeoHash
Introduction: Returns GeoHash of the geometry with given precision Format:ST_GeoHash(geom: Geometry, precision: Integer)
SQL Example
ST_GeometricMedian
Introduction: Computes the approximate geometric median of a MultiPoint geometry using the Weiszfeld algorithm. The geometric median provides a centrality measure that is less sensitive to outlier points than the centroid. The algorithm will iterate until the distance change between successive iterations is less than the suppliedtolerance parameter. If this condition has not been met after maxIter iterations, the function will produce an error and exit, unless failIfNotConverged is set to false.
If a tolerance value is not provided, a default tolerance value is 1e-6.
Format:
tolerance: 1e-6, maxIter: 1000, failIfNotConverged: false
SQL Example
ST_GeometryN
Introduction: Return the 0-based Nth geometry if the geometry is a GEOMETRYCOLLECTION, (MULTI)POINT, (MULTI)LINESTRING, MULTICURVE or (MULTI)POLYGON. Otherwise, return null Format:ST_GeometryN(geom: Geometry, n: Integer)
SQL Example
ST_GeometryType
Introduction: Returns the type of the geometry as a string. EG: ‘ST_Linestring’, ‘ST_Polygon’ etc. Format:ST_GeometryType (A: Geometry)
SQL Example
ST_GetReverseGeocodingLayers
Introduction: Returns an Array of layers that can be passed toST_ReverseGeocode. You can change the geocodes table or
view used by setting spark.sedona.reverse.geocode.table in the spark config.
the geometry must use EPSG:4326. If the SRID is set to a value other than 4326, the function will throw an exception. If the SRID is not set, the function will assume the geometry is in EPSG:4326.
ST_GetReverseGeocodingLayers()
SQL Example
ST_GLocal
Introduction: Runs Getis and Ord’s G Local (Gi or Gi*) statistic on the geometry given theweights and level.
Getis and Ord’s Gi and Gi* statistics are used to identify data points with locally high values (hot spots) and low
values (cold spots) in a spatial dataset.
The ST_WeightedDistanceBand and ST_BinaryDistanceBand functions can be used to generate the weights column.
Format: ST_GLocal(geom: Geometry, weights: Struct, level: Int)
SQL Example
ST_H3CellDistance
Introduction: return result of h3 function gridDistance(cel1, cell2). As described by H3 documentationFinding the distance can fail because the two indexes are not comparable (different resolutions), too far apart, or are separated by pentagonal distortion. This is the same set of limitations as the local IJ coordinate space functions.In this case, Sedona use in-house implementation of estimation the shortest path and return the size as distance. Format:
ST_H3CellDistance(cell1: Long, cell2: Long)
SQL Example
ST_H3CellIDs
Introduction: Cover the geometry by H3 cell IDs with the given resolution(level). To understand the cell statistics please refer to H3 Doc H3 native fill functions doesn’t guarantee full coverage on the shapes.Cover Polygon
When fullCover = false, for polygon sedona will use polygonToCells. This can’t guarantee full coverage but will guarantee no false positive. When fullCover = true, sedona will add on extra traversal logic to guarantee full coverage on shapes. This will lead to redundancy but can guarantee full coverage. Choose the option according to your use case.Cover LineString
For the lineString, sedona will call gridPathCells(https://h3geo.org/docs/api/traversal#gridpathcells) per segment. From H3’s documentationThis function may fail to find the line between two indexes, for example if they are very far apart. It may also fail when finding distances for indexes on opposite sides of a pentagon.When the
gridPathCells function throw error, Sedona implemented in-house approximate implementation to generate the shortest path, which can cover the corner cases.
Both functions can’t guarantee full coverage. When the fullCover = true, we’ll do extra cell traversal to guarantee full cover.
In worst case, sedona will use MBR to guarantee the full coverage.
If you seek to get the shortest path between cells, you can call this function with fullCover = false
Format: ST_H3CellIDs(geom: geometry, level: Int, fullCover: Boolean)
SQL Example
ST_H3KRing
Introduction: return the result of H3 function gridDisk(cell, k). K meansthe distance of the origin index, gridDisk(cell, k) return cells with distance <=k from the original cell.
exactRing : Boolean, when set to true, sedona will remove the result of gridDisk(cell, k-1) from the original results,
means only keep the cells with distance exactly k from the original cell
Format: ST_H3KRing(cell: Long, k: Int, exactRing: Boolean)
SQL Example
ST_H3ToGeom
Introduction: Return the result of H3 function cellsToMultiPolygon(cells). Converts an array of Uber H3 cell indices into an array of Polygon geometries, where each polygon represents a hexagonal H3 cell. Format:ST_H3ToGeom(cells: Array[Long])
Example:
ST_HasM
Introduction: Checks for the presence of M coordinate values representing measures or linear references. Returns true if the input geometry includes an M coordinate, false otherwise. Format:ST_HasM(geom: Geometry)
SQL Example
ST_HasZ
Introduction: Checks for the presence of Z coordinate values representing measures or linear references. Returns true if the input geometry includes an Z coordinate, false otherwise. Format:ST_HasZ(geom: Geometry)
SQL Example
ST_HausdorffDistance
Introduction: Returns a discretized (and hence approximate) Hausdorff distance between the given 2 geometries. Optionally, a densityFraction parameter can be specified, which gives more accurate results by densifying segments before computing hausdorff distance between them. Each segment is broken down into equal-length subsegments whose ratio with segment length is closest to the given density fraction. Hence, the lower the densityFrac value, the more accurate is the computed hausdorff distance, and the more time it takes to compute it. If any of the geometry is empty, 0.0 is returned.Accepted range of densityFrac is (0.0, 1.0], if any other value is provided, ST_HausdorffDistance throws an IllegalArgumentException
Even though the function accepts 3D geometry, the z ordinate is ignored and the computed hausdorff distance is equivalent to the geometries not having the z ordinate.
ST_HausdorffDistance(g1: Geometry, g2: Geometry, densityFrac: Double)
SQL Example
ST_InteriorRingN
Introduction: Returns the Nth interior linestring ring of the polygon geometry. Returns NULL if the geometry is not a polygon or the given N is out of range Format:ST_InteriorRingN(geom: Geometry, n: Integer)
SQL Example
ST_InterpolatePoint
Introduction: Returns the interpolated measure value of a linear measured LineString at the point closest to the specified point.Make sure that both geometries have the same SRID, otherwise the function will throw an IllegalArgumentException.
ST_InterpolatePoint(linestringM: Geometry, point: Geometry)
SQL Example
ST_Intersection
Introduction: Return the intersection geometry of A and B Format:ST_Intersection (A: Geometry, B: Geometry)
SQL Example
ST_IsClosed
Introduction: RETURNS true if the LINESTRING start and end point are the same. Format:ST_IsClosed(geom: Geometry)
SQL Example
ST_IsCollection
Introduction: ReturnsTRUE if the geometry type of the input is a geometry collection type.
Collection types are the following:
- GEOMETRYCOLLECTION
MULTI{POINT, POLYGON, LINESTRING}
ST_IsCollection(geom: Geometry)
SQL Example
ST_IsEmpty
Introduction: Test if a geometry is empty geometry Format:ST_IsEmpty (A: Geometry)
SQL Example
ST_Isochrone
ST_Isochrone and ST_Isochrones functions are limited to Paid Organizations.Only Professional and Enterprise Edition Organizations have access to
ST_Isochrone and ST_Isochrones.For more information on Paid Organizations, see Wherobots Pricing.
If you have already decided on using a Paid Organization, see Create a new Organization or Upgrade Organization.
time_limit (in minutes).
An isochrone is a polygon that represents the area that can be reached within a given time from the input geometry.
Format: ST_Isochrone(geometry: Geometry, time_limit: Double, mobility_type: String, inbound: Boolean)
SQL Example
geometry: The input geometry for the isochrone calculation. If the input is not a point, the centroid of the geometry will be used.time_limit: Specifies the maximum travel time, in minutes, for the generated isochrone.mobility_type: Specifies which method of travel is used in the calculation.
“Currently,
car is the only supported mobility_type.”
Currently, ST_Isochrone and ST_Isochrones only support generating isochrones for car travel.inbound: Determines how the isochrone is calculated:- If
true, the input geometry represents a destination. - If
false, the input geometry represents an origin.
- If
Best Practices for Wherobots Travel Isochrones
- Multiple Times from Same Origin? Use
ST_IsochronesFor calculating isochrones for several time limits (e.g., 10, 20, 30 mins) from the same starting point(s), useST_Isochrones(geometry, array(10, 20, 30), ...)for significantly better performance. - Avoid Repeated
ST_IsochroneCalls for the same point Don’t callST_Isochronemultiple times for the same point with different times; this is very inefficient. - Performance Varies Runtimes depend on road network density and origin point clustering. Dense/complex areas take longer.
- Choose Function
ST_Isochrone: Best for a single time limit per origin.ST_Isochrones: Best for multiple time limits per origin.
- Use this pattern
- Avoid this pattern
ST_Isochrones
`ST_Isochrone` and `ST_Isochrones` functions are limited to Paid Organizations.
`ST_Isochrone` and `ST_Isochrones` functions are limited to Paid Organizations.
Only Professional and Enterprise Edition Organizations have access to
For more information on Paid Organizations, see Wherobots Pricing.
If you have already decided on using a Paid Organization, see Create a new Organization or Upgrade Organization.
ST_Isochrone and ST_Isochrones.For more information on Paid Organizations, see Wherobots Pricing.
If you have already decided on using a Paid Organization, see Create a new Organization or Upgrade Organization.
time_limits array (in minutes). time_limits should be sorted from least to greatest.
An isochrone is a polygon that represents the area that can be reached within a given time from the input geometry.
ST_Isochrones returns an output array of geometries. Each geometry within the output array corresponds to an isochrone defined by a time limit. The geometry at index x in the output array represents the isochrone for the time limit at index x in the provided input time_limits array.
Format: ST_Isochrones(geometry: Geometry, time_limits: Array<Double>, mobility_type: String, inbound: Boolean, isolate_contours: Boolean)
geometry: The input geometry for the isochrone calculation. If the input is not a point, the centroid of the geometry will be used.time_limits:Specifies the maximum travel times, in minutes, for the generated isochrones.mobility_type: Specifies which method of travel is used in the calculation.
Currently,
Currently,
car is the only supported mobility_type.Currently,
ST_Isochrone and ST_Isochrones only support generating isochrones for car travel.inbound: Determines how the isochrone is calculated:- If
true, the input geometry represents a destination. - If
false, the input geometry represents an origin.
- If
isolate_contours: Determines if the isochrones should be overlapping the prior isochrones (isolate_contours = false) or if they should be concentric rings (isolate_contours = true).
ST_IsPolygonCCW
Introduction: Returns true if all polygonal components in the input geometry have their exterior rings oriented counter-clockwise and interior rings oriented clockwise. Format:ST_IsPolygonCCW(geom: Geometry)
SQL Example:
ST_IsPolygonCW
Introduction: Returns true if all polygonal components in the input geometry have their exterior rings oriented counter-clockwise and interior rings oriented clockwise. Format:ST_IsPolygonCW(geom: Geometry)
SQL Example:
ST_IsRing
Introduction: RETURN true if LINESTRING is ST_IsClosed and ST_IsSimple. Format:ST_IsRing(geom: Geometry)
SQL Example
ST_IsSimple
Introduction: Test if geometry’s only self-intersections are at boundary points. Format:ST_IsSimple (A: Geometry)
SQL Example
ST_IsValid
Introduction: Test if a geometry is well-formed. The function can be invoked with just the geometry or with an additional flag (fromv1.5.1). The flag alters the validity checking behavior. The flags parameter is a bitfield with the following options:
- 0 (default): Use usual OGC SFS (Simple Features Specification) validity semantics.
- 1: “ESRI flag”, Accepts certain self-touching rings as valid, which are considered invalid under OGC standards.
ST_IsValidDetail
Introduction: Returns a row, containing a booleanvalid stating if a geometry is valid, a string reason stating why it is invalid and a geometry location pointing out where it is invalid.
This function is a combination of ST_IsValid and ST_IsValidReason.
The flags parameter is a bitfield with the following options:
- 0 (default): Use usual OGC SFS (Simple Features Specification) validity semantics.
- 1: “ESRI flag”, Accepts certain self-touching rings as valid, which are considered invalid under OGC standards.
ST_IsValidReason
Introduction: Returns text stating if the geometry is valid. If not, it provides a reason why it is invalid. The function can be invoked with just the geometry or with an additional flag. The flag alters the validity checking behavior. The flags parameter is a bitfield with the following options:- 0 (default): Use usual OGC SFS (Simple Features Specification) validity semantics.
- 1: “ESRI flag”, Accepts certain self-touching rings as valid, which are considered invalid under OGC standards.
ST_IsValidTrajectory
Introduction: This function checks if a geometry is a valid trajectory representation. For a trajectory to be considered valid, it must be a LineString that includes measure (M) values. The key requirement is that the M values increase from one vertex to the next as you move along the line. Format:ST_IsValidTrajectory(geom: Geometry)
SQL Example:
ST_LabelPoint
Introduction:ST_LabelPoint computes and returns a label point for a given polygon or geometry collection. The label point is chosen to be sufficiently far from boundaries of the geometry. For a regular Polygon this will be the
centroid.
The algorithm is derived from Tippecanoe’s polygon_to_anchor, an approximate solution for label point generation, designed to be faster than optimal algorithms like polylabel. It searches for a “good enough” label point within a limited number of iterations. For geometry collections, only the largest Polygon by area is considered. While ST_Centroid is a fast algorithm to calculate the center of mass of a (Multi)Polygon, it may place the point outside of the Polygon or near a boundary for concave shapes, polygons with holes, or MultiPolygons.
ST_LabelPoint takes up to 3 arguments,
geometry: input geometry (e.g., a Polygon or GeometryCollection) for which the anchor point is to be calculated.gridResolution(Optional, default is 16): Controls the resolution of the search grid for refining the label point. A higher resolution increases the grid density, providing a higher chance of finding a good enough result at the cost of runtime. For example, a gridResolution of 16 divides the bounding box of the polygon into a 16x16 grid.goodnessThreshold(Optional, default is 0.2): Determines the minimum acceptable “goodness” value for the anchor point. Higher thresholds prioritize points farther from boundaries but may require more computation.
ST_LabelPointthrows anIllegalArgumentExceptionif the input geometry has an area of zero or less.- Holes within polygons are respected. Points within a hole are given a goodness of 0.
- For GeometryCollections, only the largest polygon by area is considered.
ST_Length
Introduction: Returns the perimeter of A. This function only supports LineString, MultiLineString, and GeometryCollections containing linear geometries. Use ST_Perimeter for polygons. Format:ST_Length (A: Geometry)
SQL Example
ST_Length2D
Introduction: Returns the perimeter of A. This function is an alias of ST_Length. This function only supports LineString, MultiLineString, and GeometryCollections containing linear geometries. Use ST_Perimeter for polygons. Format: ST_Length2D (A:geometry) SQL Example:ST_LengthSpheroid
Introduction: Return the geodesic perimeter of A using WGS84 spheroid. Unit is meter. Works better for large geometries (country level) compared toST_Length + ST_Transform. It is equivalent to PostGIS ST_Length(geography, use_spheroid=true) and ST_LengthSpheroid function and produces nearly identical results. This function only supports LineString, MultiLineString, and GeometryCollections containing linear geometries. Use ST_Perimeter for polygons.
Geometry must be in EPSG:4326 (WGS84) projection and must be in ==lon/lat== order. You can use ==ST_FlipCoordinates== to swap lat and lon.
By default, this function uses lon/lat order.
ST_LengthSpheroid (A: Geometry)
SQL Example
ST_LineFromMultiPoint
Introduction: Creates a LineString from a MultiPoint geometry. Format:ST_LineFromMultiPoint (A: Geometry)
SQL Example
ST_LineInterpolatePoint
Introduction: Returns a point interpolated along a line. First argument must be a LINESTRING. Second argument is a Double between 0 and 1 representing fraction of total linestring length the point has to be located. Format:ST_LineInterpolatePoint (geom: Geometry, fraction: Double)
SQL Example
ST_LineLocatePoint
Introduction: Returns a double between 0 and 1, representing the location of the closest point on the LineString as a fraction of its total length. The first argument must be a LINESTRING, and the second argument is a POINT geometry. Format:ST_LineLocatePoint(linestring: Geometry, point: Geometry)
SQL Example:
ST_LineMerge
Introduction: Returns a LineString formed by sewing together the constituent line work of a MULTILINESTRING.Only works for MULTILINESTRING. Using other geometry will return a GEOMETRYCOLLECTION EMPTY. If the MultiLineString can’t be merged, the original MULTILINESTRING is returned.
ST_LineMerge (A: Geometry)
SQL Example
ST_LineSegments
Introduction: This function transforms a LineString containing multiple coordinates into an array of LineStrings, each with precisely two coordinates. Thelenient argument, true by default, prevents an exception from being raised if the input geometry is not a LineString.
Format:
ST_LineSegments(geom: Geometry, lenient: Boolean)
ST_LineSegments(geom: Geometry)
SQL Example:
ST_LineSubstring
Introduction: Return a linestring being a substring of the input one starting and ending at the given fractions of total 2d length. Second and third arguments are Double values between 0 and 1. This only works with LINESTRINGs. Format:ST_LineSubstring (geom: Geometry, startfraction: Double, endfraction: Double)
SQL Example
ST_LocalOutlierFactor
Introduction: Computes the Local Outlier Factor (LOF) for each point in the input dataset. Local Outlier Factor is an algorithm for determining the degree to which a single record is an inlier or outlier. It is based on how close a record is to itsk nearest neighbors vs how close those neighbors are to their k nearest
neighbors. Values substantially less than 1 imply that the record is an inlier, while values greater than 1 imply that
the record is an outlier.
ST_LocalOutlierFactor has a useSphere parameter rather than a useSpheroid parameter. This function thus uses a spherical model of the earth rather than an ellipsoidal model when calculating distance.
ST_LocalOutlierFactor(geometry: Geometry, k: Int, useSphere: Boolean)
SQL Example
ST_LocateAlong
Introduction: This function computes Point or MultiPoint geometries representing locations along a measured input geometry (LineString or MultiLineString) corresponding to the provided measure value(s). Polygonal geometry inputs are not supported. The output points lie directly on the input line at the specified measure positions. Additionally, an optionaloffset parameter can shift the resulting points left or right from the input line. A positive offset displaces the points to the left side, while a negative value offsets them to the right side by the given distance.
This allows identifying precise locations along a measured linear geometry based on supplied measure values, with the ability to offset the output points if needed.
Format:
ST_LocateAlong(linear: Geometry, measure: Double, offset: Double)
ST_LocateAlong(linear: Geometry, measure: Double)
SQL Example:
ST_LongestLine
Introduction: Returns the LineString geometry representing the maximum distance between any two points from the input geometries. Format:ST_LongestLine(geom1: Geometry, geom2: Geometry)
SQL Example:
ST_M
Introduction: Returns M Coordinate of given Point, null otherwise. Format:ST_M(geom: Geometry)
SQL Example
ST_MMax
Introduction: Returns M maxima of the given geometry or null if there is no M coordinate. Format:ST_MMax(geom: Geometry)
SQL Example
ST_MMin
Introduction: Returns M minima of the given geometry or null if there is no M coordinate. Format:ST_MMin(geom: Geometry)
SQL Example:
ST_MakeLine
Introduction: Creates a LineString containing the points of Point, MultiPoint, or LineString geometries. Other geometry types cause an error. Format:ST_MakeLine(geom1: Geometry, geom2: Geometry)
ST_MakeLine(geoms: ARRAY[Geometry])
SQL Example
ST_MakePolygon
Introduction: Function to convert closed linestring to polygon including holes Format:ST_MakePolygon(geom: Geometry, holes: ARRAY[Geometry])
SQL Example
ST_MakeValid
Introduction: Given an invalid geometry, create a valid representation of the geometry. Collapsed geometries are either converted to empty (keepCollapsed=false) or a valid geometry of lower dimension (keepCollapsed=true). Default is keepCollapsed=false. Format:ST_MakeValid (A: Geometry)
ST_MakeValid (A: Geometry, keepCollapsed: Boolean)
SQL Example
In Sedona up to and including version 1.2 the behaviour of ST_MakeValid was different.
ST_MaximumInscribedCircle
Introduction: Finds the largest circle that is contained within a (multi)polygon, or which does not overlap any lines and points. Returns a row with fields:center- center point of the circlenearest- nearest point from the center of the circleradius- radius of the circle
ST_MaximumInscribedCircle(geometry: Geometry)
SQL Example:
ST_MaxDistance
Introduction: Calculates and returns the length value representing the maximum distance between any two points across the input geometries. This function is an alias forST_LongestDistance.
Format: ST_MaxDistance(geom1: Geometry, geom2: Geometry)
SQL Example:
ST_MinimumClearance
Introduction: The minimum clearance is a metric that quantifies a geometry’s tolerance to changes in coordinate precision or vertex positions. It represents the maximum distance by which vertices can be adjusted without introducing invalidity to the geometry’s structure. A larger minimum clearance value indicates greater robustness against such perturbations. For a geometry with a minimum clearance ofx, the following conditions hold:
- No two distinct vertices are separated by a distance less than
x. - No vertex lies within a distance
xfrom any line segment it is not an endpoint of.
Double.MAX_VALUE.
Format: ST_MinimumClearance(geometry: Geometry)
SQL Example
ST_MinimumClearanceLine
Introduction: This function returns a two-point LineString geometry representing the minimum clearance distance of the input geometry. If the input geometry does not have a defined minimum clearance, such as for single Points or coincident MultiPoints, an empty LineString geometry is returned instead. Format:ST_MinimumClearanceLine(geometry: Geometry)
SQL Example:
ST_MinimumBoundingCircle
Introduction: Returns the smallest circle polygon that contains a geometry. The optional quadrantSegments parameter determines how many segments to use per quadrant and the default number of segments is 48. Format:ST_MinimumBoundingCircle(geom: Geometry, [Optional] quadrantSegments: Integer)
SQL Example
ST_MinimumBoundingRadius
Introduction: Returns a struct containing the center point and radius of the smallest circle that contains a geometry. Format:ST_MinimumBoundingRadius(geom: Geometry)
SQL Example
ST_Multi
Introduction: Returns a MultiGeometry object based on the geometry input. ST_Multi is basically an alias for ST_Collect with one geometry. Format:ST_Multi(geom: Geometry)
SQL Example
ST_NDims
Introduction: Returns the coordinate dimension of the geometry. Format:ST_NDims(geom: Geometry)
SQL example with z coordinate:
ST_Normalize
Introduction: Returns the input geometry in its normalized form. Format:ST_Normalize(geom: Geometry)
SQL Example
ST_NPoints
Introduction: Return points of the geometry Format:ST_NPoints (A: Geometry)
SQL Example
ST_NRings
Introduction: Returns the number of rings in a Polygon or MultiPolygon. Contrary to ST_NumInteriorRings, this function also takes into account the number of exterior rings. This function returns 0 for an empty Polygon or MultiPolygon. If the geometry is not a Polygon or MultiPolygon, an IllegalArgument Exception is thrown. Format:ST_NRings(geom: Geometry)
Examples:
Input: POLYGON ((1 0, 1 1, 2 1, 2 0, 1 0))
Output: 1
Input: 'MULTIPOLYGON (((1 0, 1 6, 6 6, 6 0, 1 0), (2 1, 2 2, 3 2, 3 1, 2 1)), ((10 0, 10 6, 16 6, 16 0, 10 0), (12 1, 12 2, 13 2, 13 1, 12 1)))'
Output: 4
Input: 'POLYGON EMPTY'
Output: 0
Input: 'LINESTRING (1 0, 1 1, 2 1)'
Output: Unsupported geometry type: LineString, only Polygon or MultiPolygon geometries are supported.
ST_NumGeometries
Introduction: Returns the number of Geometries. If geometry is a GEOMETRYCOLLECTION (or MULTI*) return the number of geometries, for single geometries will return 1. Format:ST_NumGeometries (A: Geometry)
SQL Example
ST_NumInteriorRing
Introduction: Returns number of interior rings of polygon geometries. It is an alias of ST_NumInteriorRings. Format:ST_NumInteriorRing(geom: Geometry)
SQL Example
ST_NumInteriorRings
Introduction: RETURNS number of interior rings of polygon geometries. Format:ST_NumInteriorRings(geom: Geometry)
SQL Example
ST_NumPoints
Introduction: Returns number of points in a LineStringIf any other geometry is provided as an argument, an IllegalArgumentException is thrown.
Example:
SELECT ST_NumPoints(ST_GeomFromWKT('MULTIPOINT ((0 0), (1 1), (0 1), (2 2))'))Output: IllegalArgumentException: Unsupported geometry type: MultiPoint, only LineString geometry is supported.ST_NumPoints(geom: Geometry)
SQL Example
ST_Perimeter
Introduction: This function calculates the 2D perimeter of a given geometry. It supports Polygon, MultiPolygon, and GeometryCollection geometries (as long as the GeometryCollection contains polygonal geometries). For other types, it returns 0. To measure lines, use ST_Length. To get the perimeter in meters, setuse_spheroid to true. This calculates the geodesic perimeter using the WGS84 spheroid. When using use_spheroid, the lenient parameter defaults to true, assuming the geometry uses EPSG:4326. To throw an exception instead, set lenient to false.
Format:
ST_Perimeter(geom: Geometry)
ST_Perimeter(geom: Geometry, use_spheroid: Boolean)
ST_Perimeter(geom: Geometry, use_spheroid: Boolean, lenient: Boolean = True)
SQL Example:
ST_Perimeter2D
Introduction: This function calculates the 2D perimeter of a given geometry. It supports Polygon, MultiPolygon, and GeometryCollection geometries (as long as the GeometryCollection contains polygonal geometries). For other types, it returns 0. To measure lines, use ST_Length. To get the perimeter in meters, setuse_spheroid to true. This calculates the geodesic perimeter using the WGS84 spheroid. When using use_spheroid, the lenient parameter defaults to true, assuming the geometry uses EPSG:4326. To throw an exception instead, set lenient to false.
This function is an alias for ST_Perimeter.
ST_Perimeter2D(geom: Geometry)
ST_Perimeter2D(geom: Geometry, use_spheroid: Boolean)
ST_Perimeter2D(geom: Geometry, use_spheroid: Boolean, lenient: Boolean = True)
SQL Example:
ST_PointN
Introduction: Return the Nth point in a single linestring or circular linestring in the geometry. Negative values are counted backwards from the end of the LineString, so that -1 is the last point. Returns NULL if there is no linestring in the geometry. Format:ST_PointN(geom: Geometry, n: Integer)
SQL Example
ST_PointOnSurface
Introduction: Returns a POINT guaranteed to lie on the surface. Format:ST_PointOnSurface(A: Geometry)
Examples:
ST_Points
Introduction: Returns a MultiPoint geometry consisting of all the coordinates of the input geometry. It preserves duplicate points as well as M and Z coordinates. Format:ST_Points(geom: Geometry)
SQL Example
ST_Polygon
Introduction: Function to create a polygon built from the given LineString and sets the spatial reference system from the srid Format:ST_Polygon(geom: Geometry, srid: Integer)
SQL Example
ST_Polygonize
Introduction: Generates a GeometryCollection composed of polygons that are formed from the linework of an input GeometryCollection. When the input does not contain any linework that forms a polygon, the function will return an empty GeometryCollection.ST_Polygonize function assumes that the input geometries form a valid and simple closed linestring that can be turned into a polygon. If the input geometries are not noded or do not form such linestrings, the resulting GeometryCollection may be empty or may not contain the expected polygons.ST_Polygonize(geom: Geometry)
Example:
ST_Project
Introduction: Calculates a new point location given a starting point, distance, and azimuth. The azimuth indicates the direction, expressed in radians, and is measured in a clockwise manner starting from true north. The system can handle azimuth values that are negative or exceed 2π (360 degrees). The optionallenient parameter prevents an error if the input geometry is not a Point. Its default value is false.
Format:
ST_ReducePrecision
Introduction: Reduce the decimals places in the coordinates of the geometry to the given number of decimal places. The last decimal place will be rounded. This function was called ST_PrecisionReduce in versions prior to v1.5.0. Format:ST_ReducePrecision (A: Geometry, B: Integer)
SQL Example
ST_RemovePoint
Introduction: RETURN Line with removed point at given index, position can be omitted and then last one will be removed. Format:ST_RemovePoint(geom: Geometry, position: Integer)
ST_RemovePoint(geom: Geometry)
SQL Example
ST_RemoveRepeatedPoints
Introduction: This function eliminates consecutive duplicate points within a geometry, preserving endpoints of LineStrings. It operates on (Multi)LineStrings, (Multi)Polygons, and MultiPoints, processing GeometryCollection elements individually. When an optional ‘tolerance’ value is provided, vertices within that distance are also considered duplicates. Format:ST_RemoveRepeatedPoints(geom: Geometry, tolerance: Double)
ST_RemoveRepeatedPoints(geom: Geometry)
SQL Example:
ST_Reverse
Introduction: Return the geometry with vertex order reversed Format:ST_Reverse (A: Geometry)
SQL Example
ST_ReverseGeocode
Introduction: Return a reverse geocode result struct for the given geometry and layer. If no result is found for a layer, the result contains a null geometry and location field. The geometry provided should be in the WGS84 (EPSG:4326) coordinate system, i.e. lon/lat coordinates. The layers must correspond to the layers in the reverse geocode database. You can useST_GetReverseGeocodingLayers to get a list of available layers.
You can change the geocodes table or view used by setting spark.sedona.reverse.geocode.table in the spark config.
You can set the distance thresholds (in degrees) for reverse geocoding by setting
spark.sedona.reverse.geocode.distance.<layerName>. The value for layers without a specific configuration is set by
spark.sedona.reverse.geocode.distance.default. When unset the values are 0.0006 (~67 meters on the equator) for
places, 0.0003 for addresses, and 0.0 for all other layers.
Do not pass duplicate input rows. Passing duplicate input rows has undefined behavior. The concept of a duplicate
row is based on the columns input to the function call. At the time of writing the behavior is to deduplicate.
addresses: Street addressesplaces: aka points of interestdivisions-locality: See Overture documentationdivisions-country: See Overture documentationdivisions-dependency: See Overture documentationdivisions-localadmin: See Overture documentationdivisions-macrohood: See Overture documentationdivisions-county: See Overture documentationdivisions-microhood: See Overture documentationdivisions-neighborhood: See Overture documentationdivisions-region: See Overture documentation
ST_ReverseGeocode includes the following parameters:
geom: Geometry: The location that you’re querying. Provide a geometry object in accordance with the WGS84 coordinate system (using longitude and latitude).layer: String: Specifies which “layer” of information you want to search. Layers correspond to different categories of data in the reverse geocode database.
ST_ReverseGeocode (geom: Geometry, layer: String)
SQL Example
ST_GeomFromText('POINT (13.040766 47.812924)')creates a point geometry in Salzburg Austria.'addresses'is used to specify that we want to find addresses (as opposed to e.g. places or neighborhoods).
location: The name or address found at that location (e.g., “1600 Amphitheatre Parkway, Mountain View, CA” or “Google”).layer: The resulting layer (e.g., “address” or “place”).geometry: The geometry of the result.
ST_Rotate
Introduction: Rotates a geometry by a specified angle in radians counter-clockwise around a given origin point. The origin for rotation can be specified as either a POINT geometry or x and y coordinates. If the origin is not specified, the geometry is rotated around POINT(0 0). Formats;ST_Rotate (geometry: Geometry, angle: Double)
ST_Rotate (geometry: Geometry, angle: Double, originX: Double, originY: Double)
ST_Rotate (geometry: Geometry, angle: Double, pointOrigin: Geometry)
SQL Example:
ST_RotateX
Introduction: Performs a counter-clockwise rotation of the specified geometry around the X-axis by the given angle measured in radians. Format:ST_RotateX(geometry: Geometry, angle: Double)
SQL Example:
ST_RotateY
Introduction: Performs a counter-clockwise rotation of the specified geometry around the Y-axis by the given angle measured in radians. Format:ST_RotateY(geometry: Geometry, angle: Double)
SQL Example:
ST_S2CellIDs
Introduction: Cover the geometry with Google S2 Cells, return the corresponding cell IDs with the given level. The level indicates the size of cells. With a bigger level, the cells will be smaller, the coverage will be more accurate, but the result size will be exponentially increasing. Format:ST_S2CellIDs(geom: Geometry, level: Integer)
SQL Example
ST_S2ToGeom
Introduction: Returns an array of Polygons for the corresponding S2 cell IDs. Format:ST_S2ToGeom(cellIds: Array[Long])
SQL Example:
ST_Scale
Introduction: This function scales the geometry to a new size by multiplying the ordinates with the corresponding scaling factors provided as parametersscaleX and scaleY.
This function is designed for scaling 2D geometries. While it currently doesn’t support scaling the Z and M coordinates, it preserves these values during the scaling operation.
ST_Scale(geometry: Geometry, scaleX: Double, scaleY: Double)
SQL Example:
ST_ScaleGeom
Introduction: This function scales the input geometry (geometry) to a new size. It does this by multiplying the coordinates of the input geometry with corresponding values from another geometry (factor) representing the scaling factors.
To scale the geometry relative to a point other than the true origin (e.g., scaling a polygon in place using its centroid), you can use the three-geometry variant of this function. This variant requires an additional geometry (origin) representing the “false origin” for the scaling operation. If no origin is provided, the scaling occurs relative to the true origin, with all coordinates of the input geometry simply multiplied by the corresponding scale factors.
This function is designed for scaling 2D geometries. While it currently doesn’t support scaling the Z and M coordinates, it preserves these values during the scaling operation.
ST_ScaleGeom(geometry: Geometry, factor: Geometry, origin: Geometry)
ST_ScaleGeom(geometry: Geometry, factor: Geometry)
SQL Example:
ST_SetPoint
Introduction: Replace Nth point of linestring with given point. Index is 0-based. Negative index are counted backwards, e.g., -1 is last point. Format:ST_SetPoint (linestring: Geometry, index: Integer, point: Geometry)
SQL Example
ST_SetSRID
Introduction: Sets the spatial reference system identifier (SRID) of the geometry. Format:ST_SetSRID (A: Geometry, srid: Integer)
SQL Example
ST_ShiftLongitude
Introduction: Modifies longitude coordinates in geometries, shifting values between -180..0 degrees to 180..360 degrees and vice versa. This is useful for normalizing data across the International Date Line and standardizing coordinate ranges for visualization and spheroidal calculations.This function is only applicable to geometries that use lon/lat coordinate systems.
ST_ShiftLongitude (geom: geometry)
SQL example:
ST_Simplify
Introduction: This function simplifies the input geometry by applying the Douglas-Peucker algorithm.The simplification may not preserve topology, potentially producing invalid geometries. Use ST_SimplifyPreserveTopology to retain valid topology after simplification.
ST_Simplify(geom: Geometry, tolerance: Double)
SQL Example:
ST_SimplifyPolygonHull
Introduction: This function computes a topology-preserving simplified hull, either outer or inner, for a polygonal geometry input. An outer hull fully encloses the original geometry, while an inner hull lies entirely within. The result maintains the same structure as the input, including handling of MultiPolygons and holes, represented as a polygonal geometry formed from a subset of vertices. Vertex reduction is governed by thevertexFactor parameter ranging from 0 to 1, with lower values yielding simpler outputs with fewer vertices and reduced concavity. For both hull types, a vertexFactor of 1.0 returns the original geometry. Specifically, for outer hulls, 0.0 computes the convex hull; for inner hulls, 0.0 produces a triangular geometry.
The simplification algorithm iteratively removes concave corners containing the least area until reaching the target vertex count. It preserves topology by preventing edge crossings, ensuring the output is a valid polygonal geometry in all cases.
Format:
ST_SimplifyPreserveTopology
Introduction: Simplifies a geometry and ensures that the result is a valid geometry having the same dimension and number of components as the input, and with the components having the same topological relationship. Format:ST_SimplifyPreserveTopology (A: Geometry, distanceTolerance: Double)
SQL Example
ST_SimplifyVW
Introduction: This function simplifies the input geometry by applying the Visvalingam-Whyatt algorithm.The simplification may not preserve topology, potentially producing invalid geometries. Use ST_SimplifyPreserveTopology to retain valid topology after simplification.
ST_SimplifyVW(geom: Geometry, tolerance: Double)
SQL Example
ST_Snap
Introduction: Snaps the vertices and segments of theinput geometry to reference geometry within the specified tolerance distance. The tolerance parameter controls the maximum snap distance.
If the minimum distance between the geometries exceeds the tolerance, the input geometry is returned unmodified. Adjusting the tolerance value allows tuning which vertices should snap to the reference and which remain untouched.
Format: ST_Snap(input: Geometry, reference: Geometry, tolerance: double)
Input geometry:
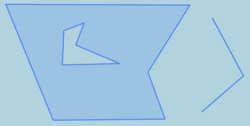
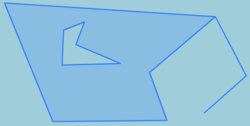
ST_Split
Introduction: Split an input geometry by another geometry (called the blade). Linear (LineString or MultiLineString) geometry can be split by a Point, MultiPoint, LineString, MultiLineString, Polygon, or MultiPolygon. Polygonal (Polygon or MultiPolygon) geometry can be split by a LineString, MultiLineString, Polygon, or MultiPolygon. In either case, when a polygonal blade is used then the boundary of the blade is what is actually split by. ST_Split will always return either a MultiLineString or MultiPolygon even if they only contain a single geometry. Homogeneous GeometryCollections are treated as a multi-geometry of the type it contains. For example, if a GeometryCollection of only Point geometries is passed as a blade it is the same as passing a MultiPoint of the same geometries. Format:ST_Split (input: Geometry, blade: Geometry)
SQL Example
ST_SRID
Introduction: Return the spatial reference system identifier (SRID) of the geometry. Format:ST_SRID (A: Geometry)
SQL Example
ST_StartPoint
Introduction: Returns first point of given linestring. Format:ST_StartPoint(geom: Geometry)
SQL Example
ST_SubDivide
Introduction: Returns list of geometries divided based of given maximum number of vertices. Format:ST_SubDivide(geom: Geometry, maxVertices: Integer)
SQL Example
ST_SubDivideExplode
Introduction: It works the same as ST_SubDivide but returns new rows with geometries instead of list. Format:ST_SubDivideExplode(geom: Geometry, maxVertices: Integer)
SQL Example
Query:
ST_SymDifference
Introduction: Return the symmetrical difference between geometry A and B (return parts of geometries which are in either of the sets, but not in their intersection) Format:ST_SymDifference (A: Geometry, B: Geometry)
SQL Example
ST_Transform
Introduction: Transform the Spatial Reference System / Coordinate Reference System of A, from SourceCRS to TargetCRS. For SourceCRS and TargetCRS, WKT format is also available. Lon/Lat Order in the input geometry If the input geometry is in lat/lon order, it might throw an error such astoo close to pole, latitude or longitude exceeded limits, or give unexpected results.
You need to make sure that the input geometry is in lon/lat order. If the input geometry is in lat/lon order, you can use ==ST_FlipCoordinates== to swap X and Y.
Lon/Lat Order in the source and target CRS
Sedona will make sure the source and target CRS to be in lon/lat order. If the source CRS or target CRS is in lat/lon order, these CRS will be swapped to lon/lat order.
CRS code
The CRS code is the code of the CRS in the official EPSG database (https://epsg.org/) in the format of EPSG:XXXX. A community tool EPSG.io can help you quick identify a CRS code. For example, the code of WGS84 is EPSG:4326.
WKT format
You can also use OGC WKT v1 format to specify the source CRS and target CRS. An example OGC WKT v1 CRS of EPGS:3857 is as follows:
By default, this function uses lon/lat order.
By default, ==ST_Transform== follows the
lenient mode which tries to fix issues by itself. You can append a boolean value at the end to enable the strict mode. In strict mode, ==ST_Transform== will throw an error if it finds any issue.ST_Translate
Introduction: Returns the input geometry with its X, Y and Z coordinates (if present in the geometry) translated by deltaX, deltaY and deltaZ (if specified) If the geometry is 2D, and a deltaZ parameter is specified, no change is done to the Z coordinate of the geometry and the resultant geometry is also 2D. If the geometry is empty, no change is done to it. If the given geometry contains sub-geometries (GEOMETRY COLLECTION, MULTI POLYGON/LINE/POINT), all underlying geometries are individually translated. Format:ST_Translate(geometry: Geometry, deltaX: Double, deltaY: Double, deltaZ: Double)
SQL Example
ST_TriangulatePolygon
Introduction: Generates the constrained Delaunay triangulation for the input Polygon. The constrained Delaunay triangulation is a set of triangles created from the Polygon’s vertices that covers the Polygon area precisely, while maximizing the combined interior angles across all triangles compared to other possible triangulations. This produces the highest quality triangulation representation of the Polygon geometry. The function returns a GeometryCollection of Polygon geometries comprising this optimized constrained Delaunay triangulation. Polygons with holes and MultiPolygon types are supported. For any other geometry type provided, such as Point, LineString, etc., an empty GeometryCollection will be returned. Format:ST_TriangulatePolygon(geom: Geometry)
SQL Example
ST_UnaryUnion
Introduction: This variant of ST_Union operates on a single geometry input. The input geometry can be a simple Geometry type, a MultiGeometry, or a GeometryCollection. The function calculates the geometric union across all components and elements within the provided geometry object. Format:ST_UnaryUnion(geometry: Geometry)
SQL Example
ST_Union
Introduction: Variant 1: Return the union of geometry A and B. Variant 2 : As of version1.6.0, this function accepts an array of Geometry objects and returns the geometric union of all geometries in the input array. If the polygons within the input array do not share common boundaries, the ST_Union result will be a MultiPolygon geometry.
Format:
ST_Union (A: Geometry, B: Geometry)
ST_Union (geoms: Array(Geometry))
SQL Example
ST_VoronoiPolygons
Introduction: Returns a two-dimensional Voronoi diagram from the vertices of the supplied geometry. The result is a GeometryCollection of Polygons that covers an envelope larger than the extent of the input vertices. Returns null if input geometry is null. Returns an empty geometry collection if the input geometry contains only one vertex. Returns an empty geometry collection if the extend_to envelope has zero area. Format:ST_VoronoiPolygons(g1: Geometry, tolerance: Double, extend_to: Geometry)
Optional parameters:
tolerance : The distance within which vertices will be considered equivalent. Robustness of the algorithm can be improved by supplying a nonzero tolerance distance. (default = 0.0)
extend_to : If a geometry is supplied as the “extend_to” parameter, the diagram will be extended to cover the envelope of the “extend_to” geometry, unless that envelope is smaller than the default envelope (default = NULL. By default, we extend the bounding box of the diagram by the max between bounding box’s height and bounding box’s width).
SQL Example
ST_WeightedDistanceBandColumn
Introduction: Introduction: Returns aweights column containing every record in a dataframe within a specified threshold distance.
The weights column is an array of structs containing the attributes from each neighbor and that neighbor’s weight. Since this is a distance weighted distance band, weights will be distance^alpha.
Format: ST_WeightedDistanceBandColumn(geometry:Geometry, threshold: Double, alpha: Double, includeZeroDistanceNeighbors: boolean, includeSelf: boolean, selfWeight: Double, useSpheroid: boolean, attributes: Struct)
SQL Example:
ST_X
Introduction: Returns X Coordinate of given Point null otherwise. Format:ST_X(pointA: Point)
SQL Example
ST_XMax
Introduction: Returns the maximum X coordinate of a geometry Format:ST_XMax (A: Geometry)
SQL Example
ST_XMin
Introduction: Returns the minimum X coordinate of a geometry Format:ST_XMin (A: Geometry)
SQL Example
ST_XZ2
Introduction: Returns the numeric index (a long integer) representing the XZ2 value. Only supports data in lon/lat format. XZ2 is a 2D space filling curve that is used to index 2D data. Compared to a GeoHash, it provides improved sorting for non-point data that takes into account the bounding box of the geometry. Format:ST_XZ2(geom: Geometry, precision: Integer)
Optional parameters:
precision : Controls the number of bits used in the XZ2 value. Larger precision values take longer to compute but provide more precision. (default = 12)
SQL Example
ST_Y
Introduction: Returns Y Coordinate of given Point, null otherwise. Format:ST_Y(pointA: Point)
SQL Example
ST_YMax
Introduction: Return the minimum Y coordinate of A Format:ST_YMax (A: Geometry)
SQL Example
ST_YMin
Introduction: Return the minimum Y coordinate of A Format:ST_Y_Min (A: Geometry)
SQL Example
ST_Z
Introduction: Returns Z Coordinate of given Point, null otherwise. Format:ST_Z(pointA: Point)
SQL Example
ST_ZMax
Introduction: Returns Z maxima of the given geometry or null if there is no Z coordinate. Format:ST_ZMax(geom: Geometry)
SQL Example
ST_ZMin
Introduction: Returns Z minima of the given geometry or null if there is no Z coordinate. Format:ST_ZMin(geom: Geometry)
SQL Example
ST_Zmflag
Introduction: Returns a code indicating the Z and M coordinate dimensions present in the input geometry. Values are: 0 = 2D, 1 = 3D-M, 2 = 3D-Z, 3 = 4D. Format:ST_Zmflag(geom: Geometry)
SQL Example